 Muchas
de las expresiones que demuestran más adelante, se basan en el postulado de
estado, mismo que indica que el estado de una sustancia simple compresible se
especifica por completo mediante cualquiera de las dos propiedades intensivas
independientes.
Muchas
de las expresiones que demuestran más adelante, se basan en el postulado de
estado, mismo que indica que el estado de una sustancia simple compresible se
especifica por completo mediante cualquiera de las dos propiedades intensivas
independientes.
En este caso, la
función f depende de x más para valores de x mayores. La
inclinación de una curva en un punto se mide por medio de la pendiente de una
recta tangente a la curva en ese punto, y es equivalente a la derivada de
la función en dicho punto definida como Derivadas Parciales
Todas las demás
propiedades en ese estado pueden expresarse en términos de esas dos
propiedades. En términos matemáticos, esto es
La variación de z(x,
y) con x cuando y se mantiene constante se llama derivada
parcial de z respecto a x, y se expresa como
*No
se utiliza los moles (n) en la fórmula ya que la constante R está dividida para
el número de moles.
Tomando en cuenta
los límites cuando Δx →0 y Δy →0 y utilizando las definiciones de
derivadas parciales, se obtiene
Esta ecuación es
la relación fundamental para la diferencial total de una variable
dependiente en términos de sus derivadas parciales respecto de variables
independientes. Esta relación puede expresarse fácilmente para incluir más
variables independientes. También se puede reescribir de la siguiente manera:
Relación de Derivadas Parciales: Ecuaciones Exactas
Luego de reescribir la
ecuación, se obtuvo que
Al tomar la derivada parcial de M
respecto a y, y de N con respecto a x, se obtiene
El orden de la derivación no tiene
importancia para las propiedades, dado que son funciones de punto continuas y
tienen derivadas exactas. Por consiguiente, las dos relaciones anteriores son
idénticas:
Ésta es una
relación importante para las derivadas parciales, y se emplea en cálculo para
probar si una diferencial dz es exacta o inexacta.
Nota: puesto que todas las
propiedades termodinámicas de una sustancia quedan determinadas por el estado
en cuestión, todas las propiedades tienen una diferencial total exacta.
Relaciones de Derivadas Parciales
En
algunas circunstancias es conveniente relacionar a varias propiedades
termodinámicas por ejemplo P = P(T,V) ;
T =T(S,V)
Ejemplo abstracto
FUENTE: Cengel, Yunus .A. & Boles, Michael A. (2011). Termodinámica. México: Mcgraw - Hill

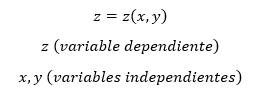
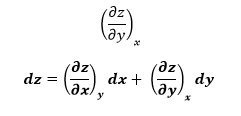


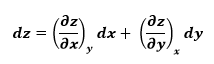








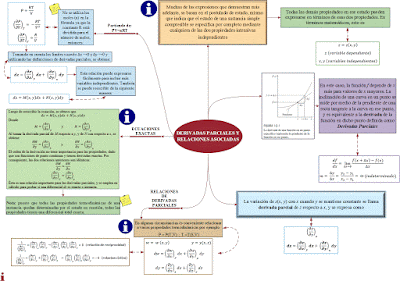
En principio la ultima demostración esta mal planteada donde dice w debe ser z por que la conclusión que es la relación cíclica sera (dx/dy)(dy/dz)(dz/dx) = -1 tambien hay error cuando se trata de igualar las derivadas mixtas de z oea (dM/dy = (dN/dx)
ResponderEliminarcorrecto amigo la relacion es para tres funciones
ResponderEliminarEsta para el oyo en5tonecs...
ResponderEliminarmal la ultima demostracion, confirmo acabo de revisar el cengel y no es asi.
ResponderEliminartenes que plantear y=y(x,w)